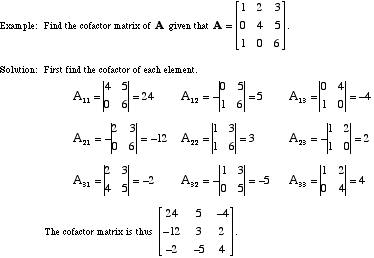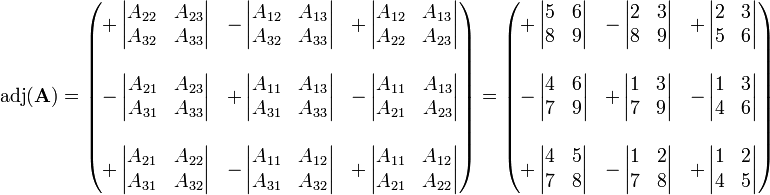3x3 Matrix Adj A Formula

The adjoint of 3x3 matrix block computes the adjoint matrix for the input matrix. This is an inverse operation. 3x3 identity matrices involves 3 rows and 3 columns.

fall outdoor welcome mats crema effaclar mat la roche posay 3 x 3 art rug magnarp floor lamp smart lights fort lauderdale cruise terminal to key west akira symphonic suite vinyl carpet seam repair tape liverpool town hall floor plan

Adjugate Matrix Computation 3x3 Linear Algebra Example Problems Youtube

$Adjugate Matrix Wikipedia$

Adjugate Matrix Wikipedia

The Classical Adjoint Of A Square Matrix

Adjoint And Inverse Of A Matrix Definition Relation Theorem Examples

Mathwords Cofactor Matrix

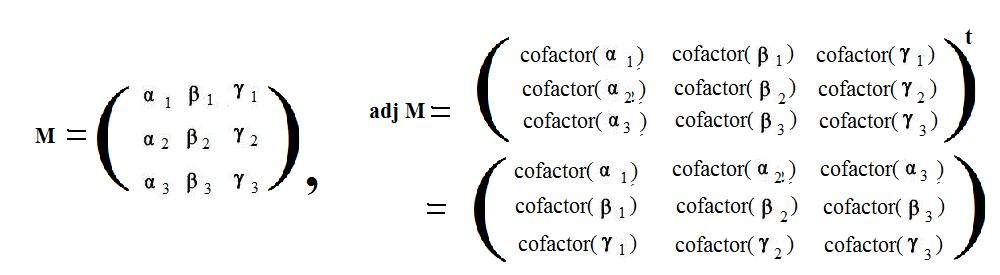
Finding Inverse Of Matrix Using Adjoint Both 2x2 And 3x3 Teachoo

$Finding Inverse Of Matrix Using Adjoint Both 2x2 And 3x3 Teachoo$

This is the currently selected item.

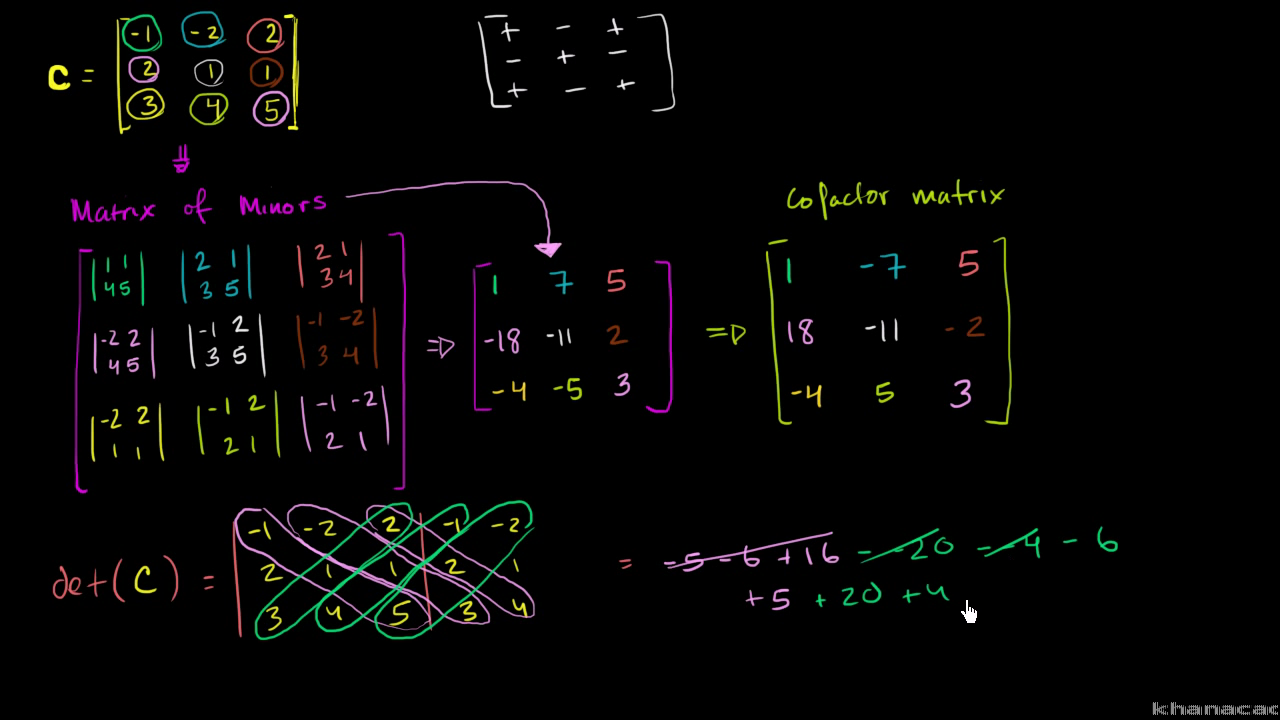
3x3 matrix adj a formula. In more detail suppose r is a commutative ring and a is an n n matrix with entries from r the i j minor of a denoted m ij is the determinant of the n 1 n 1 matrix that results from deleting row i and column j of a the cofactor matrix of a is the n n matrix c whose i j entry is the. Matrices when multiplied by its inverse will give a resultant identity matrix. The adjugate of matrix a is often written adj a. In the below inverse matrix calculator enter the values for matrix a and click calculate and calculator will provide you the adjoint adj a determinant a and inverse of a 3x3 matrix.

The name has changed to avoid ambiguity with a different defintition of the term adjoint. Inverting a 3x3 matrix using determinants part 2. When a is invertible then its inverse can be obtained by the formula given below. A singular matrix is the one in which the determinant is not equal to zero.

The matrix formed by taking the transpose of the cofactor matrix of a given original matrix. The matrix adj a is called the adjoint of matrix a. In the past the term for adjugate used to be adjoint. For related equations see algorithms.

Elements of the matrix are the numbers which make up the matrix. The inverse is defined only for non singular square matrices. Calculating the inverse of a 3x3 matrix by hand is a tedious job but worth reviewing. A 3 x 3 matrix has 3 rows and 3 columns.

Matrix of minors and cofactor matrix. For example if a problem requires you to divide by a fraction you can more easily multiply by its reciprocal. Input matrix specified as a 3 by 3 matrix in initial acceleration units. Similarly since there is no division operator for matrices you need to multiply by the inverse matrix.

The adjugate of a is the transpose of the cofactor matrix c of a. The following relationship holds between a matrix and its inverse. To find the inverse of a 3 by 3 matrix is a little critical job but can be evaluated by following few steps. Let s consider the n x n matrix a aij and define the n x n matrix adj a a t.

Port 1 input matrix 3 by 3 matrix. Inverse of a 3x3 matrix. Inverting a 3x3 matrix using determinants part 1. Solving equations with inverse matrices.