Inverse 3x3 Matrix General Formula

Finding inverse of 3x3 matrix examples. Elements of the matrix are the numbers which make up the matrix. If there exists a square matrix b of order n such that.

carpet cleaning services images magic garden ceramics mac selfridges 3rd floor marines rugged brown cover hat hand scraped luxury vinyl plank flooring area rug with green accents lt davis flooring heber springs ar custom rubber bar mats

Matrix Inverse From Wolfram Mathworld

Inverse Of A 3x3 Matrix Youtube

Quicker Way To Inverse 3 3 Matrix Math Online Tom Circle

Inverting A 3x3 Matrix Using Determinants Part 1 Matrix Of Minors And Cofactor Matrix Video Khan Academy

The Determinant Of A 3 X 3 Matrix General Shortcut Method Studypug

Matrices Algebra All Content Math Khan Academy

Inverse of a 2 2 matrix.

Inverse 3x3 matrix general formula. For example if a problem requires you to divide by a fraction you can more easily multiply by its reciprocal. Just to provide you with the general idea two matrices are inverses of each other if their product is the identity matrix. A is row equivalent to the n by n identity matrix i n. The following statements are equivalent i e they are either all true or all false for any given matrix.

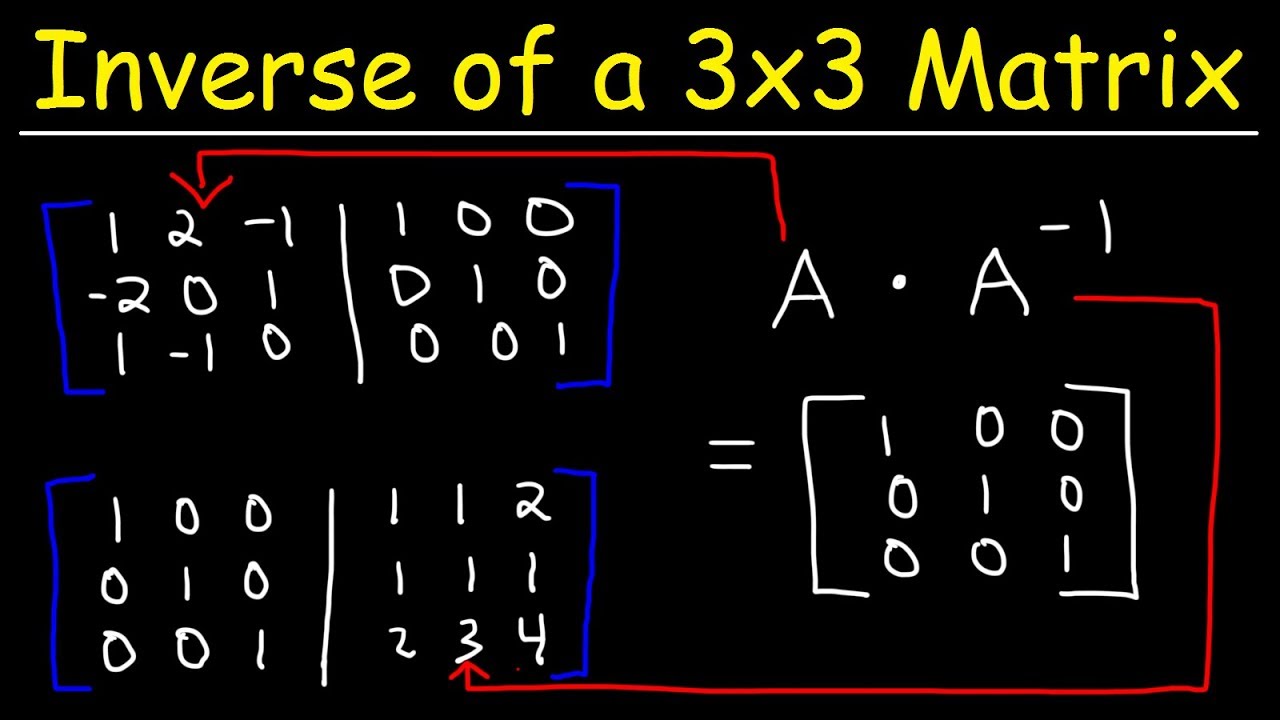
To find the inverse of a 3 by 3 matrix is a little critical job but can be evaluated by following few steps. Ab ba i n then the matrix b is called an inverse of a. Inverse of a 3 by 3 matrix as you know every 2 by 2 matrix a that isn t singular. Calculating the inverse of a 3x3 matrix by hand is a tedious job but worth reviewing.

A is invertible that is a has an inverse is nonsingular or is nondegenerate. The formula to find out the inverse of a matrix is given as. The general way to calculate the inverse of any square matrix is to append a unity matrix after the matrix i e. Inverse of a matrix is an important operation in the case of a square matrix.

Similarly since there is no division operator for matrices you need to multiply by the inverse matrix. If we know this inverse it s in general very useful. It is applicable only for a square matrix. Let a be a square matrix of order n.

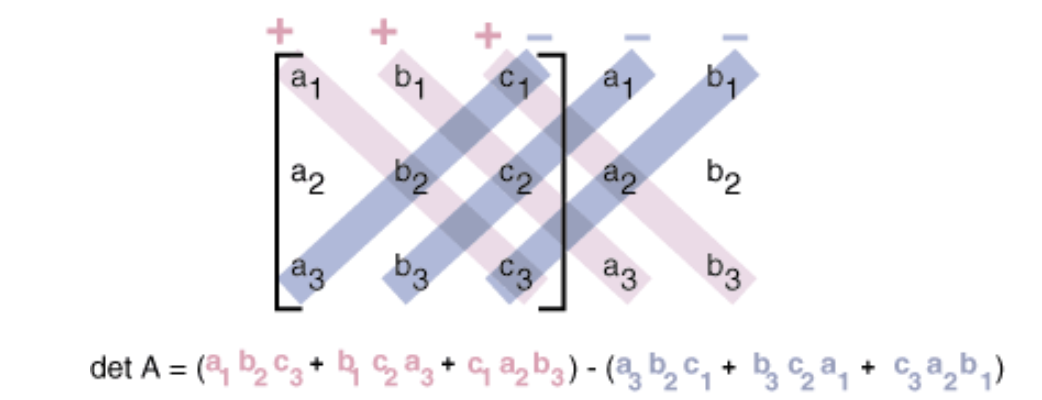
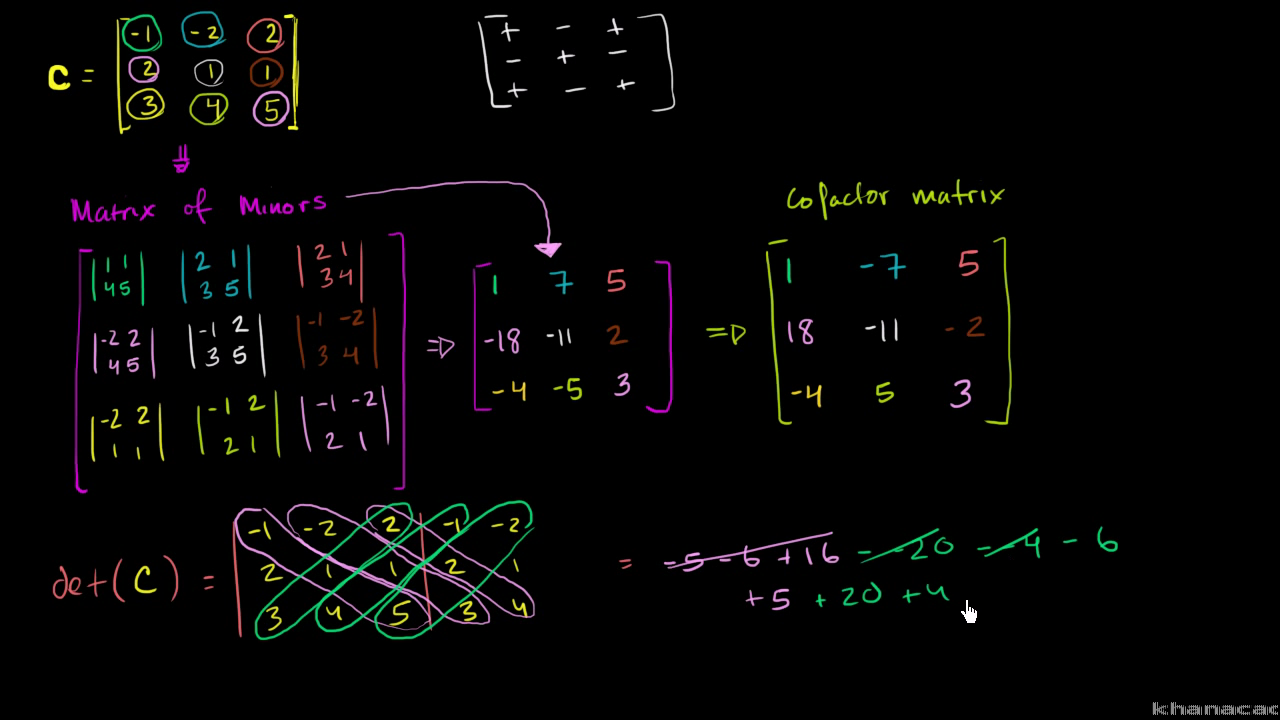
Sal shows how to find the inverse of a 3x3 matrix using its determinant. There is also a general formula based on matrix conjugates and the determinant. Adjoint is given by the transpose of cofactor of the particular matrix. In part 1 we learn how to find the matrix of minors of a 3x3 matrix and its cofactor matrix.

General formula for the inverse of a 3 3 matrix friday 18th july 2008 tuesday 29th july 2008 ben duffield cofactors determinant inverse matrix law of alternating signs maths matrix minors. If you re seeing this message it means we re having trouble loading external resources on our website. To calculate the inverse one has to find out the determinant and adjoint of that given matrix. This is an inverse operation.

A i and then do a row reduction until the matrix is of the form i b and then b is the inverse of a. For those people who need instant formulas. A singular matrix is the one in which the determinant is not equal to zero. For example it turns out that the inverse of the matrix left begin array ccc 0 3 2 1 4 2 3 4 1 end array right.

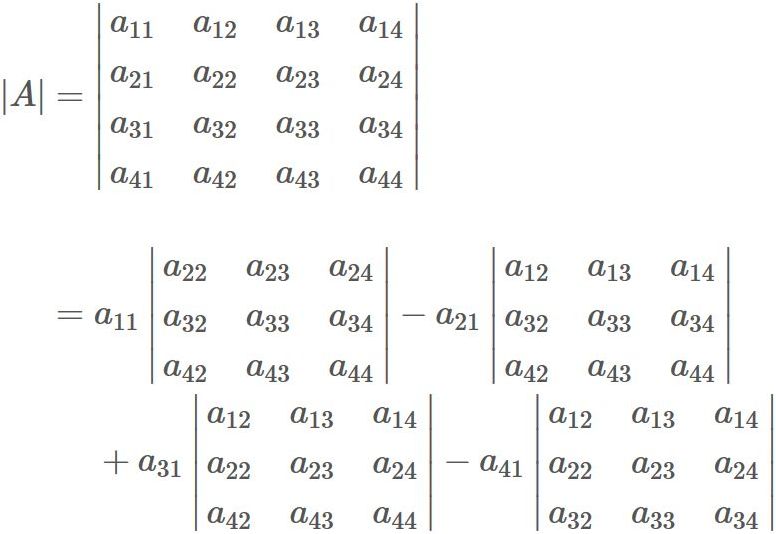
For larger square matrices there does not exist any neat formula for the. A 3 x 3 matrix has 3 rows and 3 columns. Here we are going to see some example problems of finding inverse of 3x3 matrix examples. Let a be square matrix of order n.

Properties the invertible matrix theorem. Let a be a square n by n matrix over a field k e g the field r of real numbers. In this lesson we are only going to deal with 2 2 square matrices i have prepared five 5 worked examples to illustrate the procedure on how to solve or find the inverse matrix using the formula method.